Digital Communication Channels

The communication channel provides a connection through which the information-bearing signal prop-agates. It is perhaps the most important component of a communication system. The design of all other components in Figure 0.1 depends heavily on the characteristics of the communication channel. There are many different types of physical communication channels, such as: 

1. Wire line channels 

2. Wireless channels 

3. Fiber optic channels 

4. Underwater acoustic channels 

5. Storage channels 

Different kinds of channels can have very different characteristics. In order to design an “efficient” digital communication system over a specific communication channel, we need to study the characteristics of the channel extensively and carefully. Unfortunately, this is impractical for our general treatment on digital communication theory. Instead, we adopt a model-based approach here, i.e., we construct a generic mathematical channel model to represent a "typical" communication channel. For this purpose, our channel model describes the physical communication channel as well as the properties of the equipments, such as antennas and amplifiers, necessary to access the channel. The model not only needs to be general enough to approximate most of the physical channels described above, but also simple enough to facilitate the analysis and design of the communication system. To this end, we notice that the major characteristic of a communication channel we are interested in is how the channel distorts the information-bearing signal. 

We start by listing out some common channel defects: 

1. Thermal noise in the electronic devices 

2. Signal attenuation 

3. Amplitude and phase distortion 

4. Multi path distortion 

5. Finite-bandwidth (low pass-filter) distortion 

6. Impulsive noise 

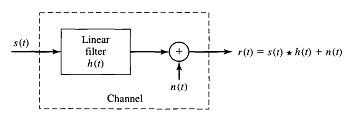
Based on knowledge of these channel defects, we construct the generic channel model. Suppose we use the symbol s(t) to denote the transmitted signal at the output of the modulator, then it is found that the following linear filter model (see Figure 1.2) sufficiently approximates the behaviors of many typical communication channels:

Where r(t) represents the received signal at the input of the demodulator, n(t) is a random process which models the thermal and impulsive noises, and c(z; t) is a linear time- varying filter 2 which models the other channel distortions listed above. We note that the linear (time-varying) channel model in (1) is very general and we work with simplifications of this model in many cases. Among the various common simplifications of the general model, the additive white Gaussian noise (AWGN) model is perhaps the most studied and important. In the AWGN model, c(;t) =δ() and (1) reduces to 

r(t)=s(t)+n(t); (2)

Where n(t) is a zero-mean wide-sense stationary Gaussian random process with auto-correlation function. 

Rn()=(Nο/2) *δ() 

 Figure 1.2

The factor No/2 is called the two-sided noise spectral density of the noise n(t). This model is primarily employed to represent the situation in which the only channel defect is the thermal noise in the electronic devices of a communication system. Although AWGN channels are rare in practice (except in deep space communications), because of its simplicity, we use the AWGN model as the cornerstone of our introduction to digital communications.